Statistik 2C: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
 
(66 mellanliggande sidversioner av 2 användare visas inte)
Rad 1: Rad 1:
== Histogram ==
== Histogram ==


Gör uppgiften nedan genom att använda Excel eller GeoGebra.
=== Exempel på histogram till uppgiften ovan===


<pdf>Statistik_i_en_klass_exempel_histogramuppgift.pdf</pdf>
[[Fil:Histogram3.PNG|400px|Så här kan det se ut om man gör histogrammet i Excel.]]


Spara Excel som pdf och ladda upp filen här på wikiskola. Lägg en länk till filen.
Histogrammet i Excel.
 
[[Fil:Histogram3.PNG|right|400px]]
Som i bilden till höger kan det se ut.
{{clear}}
{{clear}}


=== Exempel ===
=== Exempeluppgift ===


<pdf>Medelvarde-08052012125522.pdf</pdf>
<pdf>Medelvarde-08052012125522.pdf</pdf>
Rad 17: Rad 14:
=== Övning ===
=== Övning ===


[http://www.malinc.se/math/statistics/barchartssv.php  malin C - Övning GeoGebra]
här kan du lära dig skapa stapeldiagram i Geogebra
{{GGB |
[http://www.malinc.se/math/statistics/barchartssv.php  Malin C - Övning Stapeldiagram]
}}


== Statistik i GeoGebra ==
== Statistik i GeoGebra ==
Rad 26: Rad 26:


Siffrorna ovan kan man exempelvis klippa in i GGB och sedan klicka analysknappen. Ger automatiskt histogram och standardavvikelse och allt man kan begöära. Vi kan ha det som grund för alla undervisning.
Siffrorna ovan kan man exempelvis klippa in i GGB och sedan klicka analysknappen. Ger automatiskt histogram och standardavvikelse och allt man kan begöära. Vi kan ha det som grund för alla undervisning.
'''Tips''': Det borde finnas enklare sätt att få in data men om man kopiera direkt hamnar alla tal i en ruta. Sätter man däremot listan mellan måsvingar så skapaas en lista.
: <nowiki>{4, 3, 5, 6, 7, 8, 9, 9, 11, 12, 3, 4}</nowiki>
Tryck nu visa kalkylblad och dra din lista in i en ruta. Vips så har du dina data separerade.
'''En variant''': Skapa listan och skriv följande i kommandoraden så får du ditt diagram i ritfönstret:
: <nowiki>BoxPlot[0,1,{4, 3, 5, 6, 7, 8, 9, 9, 11, 12, 3, 4}]</nowiki>
I detta exempel kan du ersätta listan med namnet på en lista. Du kan även leta rätt på andra kommandon för histogram eller vad du nu vill skapa. Börjar du skriva på kommandoraden så får du förslag från GGB.


== Varationsbredd och låddiagram ==
== Varationsbredd och låddiagram ==
[[Fil:Skolinspektionen anv lådagram.PNG|400px|höger]]


'''Några spridningsmått''' Sidorna 217-221.
'''Några spridningsmått''' Sidorna 217-221.
{{svwp|Lådagram}}
{{clear}}
{{clear}}


== Standardavvikelse ==
== Standardavvikelse ==


<ggb_applet width="523" height="393" version="4.0" ggbBase64="UEsDBBQACAAIABOxrkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIABSxrkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VrdbuM2Fr6ePgWhi8UUGNukSP0460wxtjs7A2S6RT1bLPZiAFpibDay5EqU42zbt9k32RfbQ1KSpSib2M00QCdBFInk4fnjOR8PpUy+2W8StBN5IbP03CFD7CCRRlks09W5U6rLQeh88/qryUpkK7HMObrM8g1X5w7TlDI+dyIceRyH/kAESz5gARWDZUjpIGCuR8XlMsSMOAjtC3mWZt/xjSi2PBKLaC02/CKLuDKC10ptz0aj6+vrYS1qmOWr0Wq1HO6L2EGgZlqcO9XDGbDrTLqmhtzFmIz++eHCsh/ItFA8jYSDtAmlfP3Vi8m1TOPsGl3LWK3PHY+CcmshV2ulG76DRppoCw7ZikjJnShgaqtpbFabrWPIeKrHX9gnlDTmOCiWOxmL/NzBQ4YpJpSErh8wMh6DjCyXIlUVLalkjmpuk50U15atfjISgWgnC7lMxLlzyZMCTJLpZQ7ubNqFuknEkudNx0Ed8orCuPw3EBMM62Z9YBqv9OXDxfTAqCuVOUhlWWKYYvTrr8jFLkav9I3Ymws337dD2PZham+uvTF78ywNs9OZJWWWhlkaRltGqrw80cbaQs+lx1voPsqvjVddwvoyXe9umcS/R6i1+xg7iddaSRBlfs3Vk0jvM/O2RNt+nECfPYmJk1GdKpMqTlGx1rRV9CixKXTk0jHyxjoACfIgSv0A4s1DZAy3wEUQl4h4iHnQJCHy9T1ANIABhigKkaYjFJkw9UL4wwLDzEceMNO9AWQHIiCIIY8iYqKbIYhpZDIEssWlQOF5yINJWjxxNQvqI+ZDi4aIgY46OQIChBQmQhvEu4gSRPVkEiDXR77mR5hOOj/UqgNLF/kY+UQzhPyC3LJ5BfQhotqaGtZkui1Vx0XRJq4fVbZt1gKoAY8OqGfxqQOKLyYJX4oE9omFXkmEdjzRGWEEXWapQvUi+rZvlfPtWkbFQigFswr0E9/xC67E/i1QF7VsQxtlafF9nqlZlpSbtEAoyhLc6JwlpPXsNlpDg7YGWHvAaw34refgTrkZjKCyECA/y4uanMfxe01xgAbw5N/T5GaaC361zWTXjMnIbDkTUUaJjCVPf4Rg1VK0X1C9AxlAbnYgd1wrkuXx4qaACEb7f4k80xjjDXHrR0POjR2ihA3HrZ9QA1PEdfJ5uDMJ6y3uphpj486scVitlNg1a8T3ojF/lcu4/fy+mGZJ3DjD2D/jW1XmpngAHXJt1Zt0lQgTIyazYWeOrpbZfmGDg1peH2+20MJW/nJl/I4AG1zPAwK4Y7B2qRGhijCtWEOFDQ02FLiONhn3uOjZHS4Qvla1ylBSW0lwLUYWBtGw08kbE/t6ny9TqS7qhpLR1cFSTf9duVmKJoK6LMlnYjkZ3YqwSbGFgIyLtRDqzpgzW2Qdc9T3rGIw6XImkmTRJg1a0ekGlrDF3iZo7aE6pAN8HyE9EGK3IhSJBpYsRWi9iPIsSQy/Xes5MgxsWNldtlpCfpOVGmzANW+hOC0TPm3tKrr7b63A1e13lu30sNvp3h/v7J2CsELk30NtlnSYWoPegX2iM+EH4G86UQMbSZJdLwA5JU++jaXKDtqZoY+wdX2U2ybPxM8ljP4AN5mLuAMovYWdXIkcNKuwC3K2zMrCQnEL1mKQvYGmHah8znVe/gNizfbGYpWLOkQTU4HbzDCjuA1LvW7D6m2ebd6nu4+Q9LcUmIxqLSdFlMuthha0hP3+6mAeFMwFh3KhY68GW/CJjQwllc4CcFqp1tqHMAd2D7hrjE3EBkpqpAyOpOVG5DJqcmoamHIdtCorxQkBXKxiDxYNZcufIAAPtYid13IhEPwfuIFF3K65LvRJE5Gw+m3/GHYfsrgWXnsNFsWYBjC/tfm9FcIig6oAEW2BncHTljK83MtE8vzG8msBgXXDww7xew7B9Fk7xOs7hDxrh7C+Q553ytDbDhk/74xxn50/9rD7FvpFWeMD4Aq9585ffi4z9dfkv/9JV7F9NpO7HoSTjnJaUz+vp/CRnsKtExoUNvLyUNXUxzV7Nq9I7/fArOuB4komScqP9MHsy/DBm7Djg0W52fDjHAAz/3wOiDKwL41Ral7mgLXO4dUCxxoYzqbVQQEK86Y3tHyq2Q/DS3gbXvzD/nM0cjyQvuNq4aYhGlUvSR5Sa3zPtngCoP0uuJm5tb4uGiBSvQV7QONZD6cHwSkK48coTGuF6QkK9zbaJ1SY1QqzExTulUonRcSj9PVqfb0T9O3Xuk+mr1/r65+gb++wQp9M36DWNzhB3/5p88kCYl5DxMz99NL9+hh15z2AYOOnQrR5DRAzerS6PXh4QnVreJixo9V9HDg8StsaHGbe0do+DhoepW0NDTP/aG17wPB0kVADwyw4Wts7YOEPioWHSrS5ezbvl2jzE0u0ea9Ec3H4mUu0+d3ni0/ucQX2/As5YZCuGxYK1ofnMd/t5JUAtkceN8iX4Y4LWShee+SXqfsKTSlcDC4PLh+u4Le7UjKBic4tLj2HdL7G3OsPUw/8zhcWdW/zAUqtZXSVgqHmnxKadxX64Z2MY5E2LznMhzbzkab9ydX2Hl7ND47IrjfjTlh9ELFIjgyl8Z8wkm7B4vwWKlYB0Tu5EnLi0bVKsxYwesMwDEKGvSDwPBIy/4mqwQY3Xs71Edf7+tNLPPSO2676VvhDxsYh9sk49GkYsj9i6xq1v/mYb+jVv4O9/h9QSwcI918nTu4HAACrJgAAUEsBAhQAFAAIAAgAE7GuQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAUsa5A918nTu4HAACrJgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAIUIAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
[[Fil:Standardavvikels_i_Geogebra.png|440px|right]]
<br>
 
'''Tips''': Testa [http://www.wolframalpha.com/input/?i=standard+deviation+93+93+100+101+103+110&t=esm01 standard deviation i WolframAlpha]
Så här kan det se ut i Geogebra om du beräknar standardavvikelsen själv. Till höger är bara en bild. Om du vill se GGB-filen klickar du på länken nedan.
 
{{GGB|[[Standardavvikelse - uppgift i Geogebra]] }}
 
Här är ett exempel där man använder Geogebras funktion för att beräkna standrdavikelsen:
 
{{GGB | '''Medelvärde och standardavvikelse'''
 
[https://www.geogebratube.org/student/m10956 Exempel på stapeldiagram.]
}}
 
{{uppgruta  | '''<big>När började polarisarna smälta</big>'''
 
Följ länken till [http://nsidc.org/arcticseaicenews/charctic-interactive-sea-ice-graph/ Arctic Sea Ice News & Analysis]
 
Undersök vilket år isens areae hamnade utanför två standardavvikelser från medelvärdet under åren 1979-2000.
 
}}
 
{{clear}}
 
== Normalfördelningen ==
[[File:Normal distribution.svg|thumb|Normal distribution]]
 
=== Gemensam övningsuppgift ===
 
Testa dessa data i GGB:
 
85, 87, 150, 100, 100, 90, 70, 72, 75, 70, 85, 143, 100, 121, 92, 66, 70, 69, 75, 80, 140, 92, 130, 83, 70, 68, 67, 75, 83, 149, 95, 130, 80, 68, 85, 75, 73, 78, 140, 90, 124, 86, 69, 70, 75, 77, 110, 165, 110, 150, 110, 115, 80, 75, 75, 98, 172, 110, 145, 110, 95, 52, 80, 96, 110, 168, 110, 145, 110, 80,80, 75, 89, 95, 170, 110, 145, 120, 89, 72, 79, 75, 95, 220, 100, 149, 100, 110,80, 85, 80, 90, 165, 103, 135, 95, 77, 76, 85, 80, 88, 155, 103, 120, 85, 79, 78, 82, 75, 85, 150, 103, 135, 90, 75, 85, 78, 75, 88, 150, 95, 130, 90, 70, 76, 89, 82, 95, 145, 100, 133, 90, 77, 89, 79, 80, 90, 165, 103, 135, 95, 77, 86, 80, 85, 100, 160, 120, 140, 100, 90, 79, 92, 70, 100, 165, 120, 140, 100, 120, 86, 71, 95, 100, 155, 120, 139, 100, 89, 86, 78, 78, 110, 158, 122, 145, 108, 95, 95, 78
 
Är de normalfördelade?
{{clear}}
 
=== Skapa värden i Excel ===
 
Övning i att generera egna värden i Excel.
Använd [[Media:Generera_summan_av_två_slumptal.xls|denna fil]] till att generera slumptal.
 
Excel genererar två slumptal mellan 1-6. Sedan adderas de. Dessa värden ska du undersöka fördelningen av.
 
# Plocka in dem i GGB för att göra ett histogram.
# Är de normalfördelade?
 
Hur många värden behöver du för att det ska se bra ut jämfört med normalförelningskurvan?
 
Testa även att generera slumptal i GGB.
 
=== Normalfördelningskurva i GGB ===
 
[[Fil:Normalfördelning_i_GGB.png | 440 | right ]]
{{GGB|
[[Normalfördelningskurva i GGB]]
}}
{{clear}}
 
=== Intressant och lärorik överkursuppgift ===
[[Image:Normal distribution pdf.png|400px|A plot of the normal distribution, generated by gnuplot]]
 
Läs [http://en.wikipedia.org/wiki/Wikipedia:How_to_create_charts_for_Wikipedia_articles#Plotting artikeln ] och lär dig hur man skapar svg i gnuplot:
{{clear}}
 
=== Andelar i respektive kvartil ===
[[File:The Normal Distribution.svg|400px|The Normal Distribution]]
 
Mellan medelvärdet och en standardavvikelse ligger 34 % av värdena.
{{clear}}
 
=== Övning ===
 
här kan du läsa om normalfördelningen och testa hur den uppför sig i Geogebra
{{GGB |
[http://www.malinc.se/math/statistics/normal_distrsv.php  Malin C - teori om normalfördelning]
}}
 
=== Pascals triangel ===
 
Återknyt
 
=== Övrigt/Annat ===
 
Simulering av räknesticka för att åskådliggöra logaritmer
 
=== e ===
 
* [https://www.google.se/search?q=e&ie=utf-8&oe=utf-8&aq=t&rls=org.mozilla:sv-SE:official&client=firefox-a e = 2,71828183]
* [http://www.wolframalpha.com/input/?i=e^-.1304&t=esm01 e^-.1304 på Wolfram]
 
== Regression ==
 
=== Övning ===
 
här kan du lära dig regression i Geogebra
{{GGB |
[http://www.malinc.se/math/statistics/regressionsv.php  Malin C - Övning Regression]
}}
 
=== Linjär regression med GGB ===
 
* http://www.geogebratube.org/student/m14559
* http://www.geogebratube.org/material/show/id/34178
 
=== Pendellabb ===
 
[[Fil:Pendellabb_regression_Ma2C.png | right | 340px]]
 
Första kolumnen visar snörets längd för en pendel. I andra kolumnen visas tiden för fem svängningar. Därefter räknas svängningstiden för en svängning ut. I GGB kan man göra regression och pröva räta linjen, en andragradsfunktion och en potensfunktion.
 
{{clear}}
 
== NP-uppgifter ==
 
Länk finns även på NP-avsnittet.
 
* Här är en serie uppgifter på Statistik, något som man ofta inte hinner öva så mycket på. De är i en PPT:
 
{{PPT |
: [[Media:Statistik_sammanfattning_med_NP-uppgifter.pptx | Statistikuppgifter med lösningar]] }}

Nuvarande version från 8 december 2017 kl. 12.39

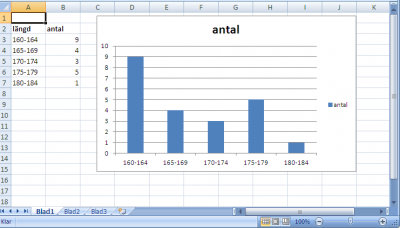
Histogram

Exempel på histogram till uppgiften ovan

Så här kan det se ut om man gör histogrammet i Excel.

Histogrammet i Excel.

Exempeluppgift

Övning

här kan du lära dig skapa stapeldiagram i Geogebra

Geogebra Undersök med Geogebra-applet: Malin C - Övning Stapeldiagram


Statistik i GeoGebra

Det går alldeles utmärkt att göra histogram och annat i GGB. 

1, 1, 2, 3, 2, 4, 3, 3, 2, 1, 4, 3, 5, 6, 7, 8, 9, 9, 11, 12, 3, 4

Siffrorna ovan kan man exempelvis klippa in i GGB och sedan klicka analysknappen. Ger automatiskt histogram och standardavvikelse och allt man kan begöära. Vi kan ha det som grund för alla undervisning.

Tips: Det borde finnas enklare sätt att få in data men om man kopiera direkt hamnar alla tal i en ruta. Sätter man däremot listan mellan måsvingar så skapaas en lista.

{4, 3, 5, 6, 7, 8, 9, 9, 11, 12, 3, 4}

Tryck nu visa kalkylblad och dra din lista in i en ruta. Vips så har du dina data separerade.

En variant: Skapa listan och skriv följande i kommandoraden så får du ditt diagram i ritfönstret:

BoxPlot[0,1,{4, 3, 5, 6, 7, 8, 9, 9, 11, 12, 3, 4}]

I detta exempel kan du ersätta listan med namnet på en lista. Du kan även leta rätt på andra kommandon för histogram eller vad du nu vill skapa. Börjar du skriva på kommandoraden så får du förslag från GGB.

Varationsbredd och låddiagram

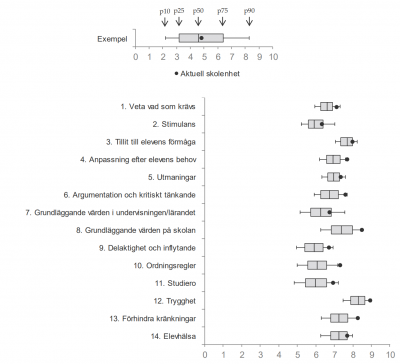
Några spridningsmått Sidorna 217-221.

Wikipedia skriver om Lådagram

Standardavvikelse

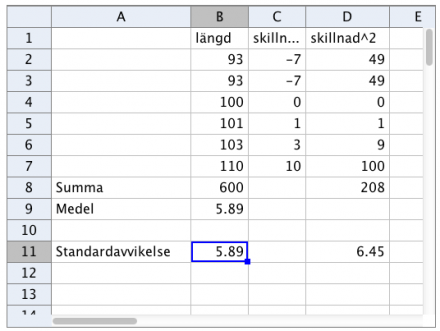
Så här kan det se ut i Geogebra om du beräknar standardavvikelsen själv. Till höger är bara en bild. Om du vill se GGB-filen klickar du på länken nedan.

Geogebra Undersök med Geogebra-applet: Standardavvikelse - uppgift i Geogebra


Här är ett exempel där man använder Geogebras funktion för att beräkna standrdavikelsen:

Geogebra Undersök med Geogebra-applet: Medelvärde och standardavvikelse

Exempel på stapeldiagram.


Uppgift
När började polarisarna smälta

Följ länken till Arctic Sea Ice News & Analysis

Undersök vilket år isens areae hamnade utanför två standardavvikelser från medelvärdet under åren 1979-2000.



Normalfördelningen

Normal distribution

Gemensam övningsuppgift

Testa dessa data i GGB:

85, 87, 150, 100, 100, 90, 70, 72, 75, 70, 85, 143, 100, 121, 92, 66, 70, 69, 75, 80, 140, 92, 130, 83, 70, 68, 67, 75, 83, 149, 95, 130, 80, 68, 85, 75, 73, 78, 140, 90, 124, 86, 69, 70, 75, 77, 110, 165, 110, 150, 110, 115, 80, 75, 75, 98, 172, 110, 145, 110, 95, 52, 80, 96, 110, 168, 110, 145, 110, 80,80, 75, 89, 95, 170, 110, 145, 120, 89, 72, 79, 75, 95, 220, 100, 149, 100, 110,80, 85, 80, 90, 165, 103, 135, 95, 77, 76, 85, 80, 88, 155, 103, 120, 85, 79, 78, 82, 75, 85, 150, 103, 135, 90, 75, 85, 78, 75, 88, 150, 95, 130, 90, 70, 76, 89, 82, 95, 145, 100, 133, 90, 77, 89, 79, 80, 90, 165, 103, 135, 95, 77, 86, 80, 85, 100, 160, 120, 140, 100, 90, 79, 92, 70, 100, 165, 120, 140, 100, 120, 86, 71, 95, 100, 155, 120, 139, 100, 89, 86, 78, 78, 110, 158, 122, 145, 108, 95, 95, 78

Är de normalfördelade?

Skapa värden i Excel

Övning i att generera egna värden i Excel.

Använd denna fil till att generera slumptal.

Excel genererar två slumptal mellan 1-6. Sedan adderas de. Dessa värden ska du undersöka fördelningen av.

  1. Plocka in dem i GGB för att göra ett histogram.
  2. Är de normalfördelade?

Hur många värden behöver du för att det ska se bra ut jämfört med normalförelningskurvan?

Testa även att generera slumptal i GGB.

Normalfördelningskurva i GGB

440
440

Geogebra Undersök med Geogebra-applet: Normalfördelningskurva i GGB

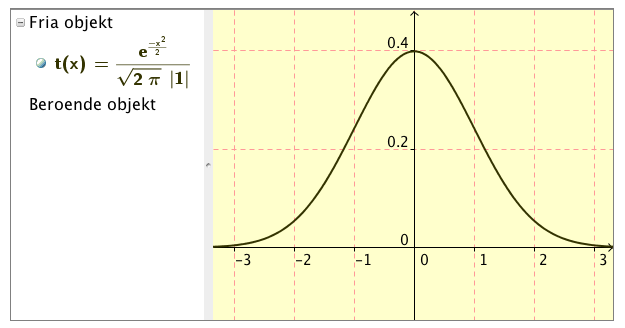
Intressant och lärorik överkursuppgift

A plot of the normal distribution, generated by gnuplot

Läs artikeln och lär dig hur man skapar svg i gnuplot:

Andelar i respektive kvartil

The Normal Distribution

Mellan medelvärdet och en standardavvikelse ligger 34 % av värdena.

Övning

här kan du läsa om normalfördelningen och testa hur den uppför sig i Geogebra

Geogebra Undersök med Geogebra-applet: Malin C - teori om normalfördelning


Pascals triangel

Återknyt

Övrigt/Annat

Simulering av räknesticka för att åskådliggöra logaritmer

e

Regression

Övning

här kan du lära dig regression i Geogebra

Geogebra Undersök med Geogebra-applet: Malin C - Övning Regression


Linjär regression med GGB

Pendellabb

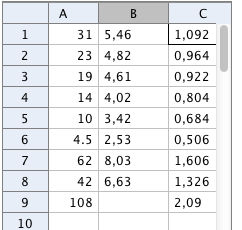
Första kolumnen visar snörets längd för en pendel. I andra kolumnen visas tiden för fem svängningar. Därefter räknas svängningstiden för en svängning ut. I GGB kan man göra regression och pröva räta linjen, en andragradsfunktion och en potensfunktion.

NP-uppgifter

Länk finns även på NP-avsnittet.

  • Här är en serie uppgifter på Statistik, något som man ofta inte hinner öva så mycket på. De är i en PPT:

Se en PowwerPoint!

Statistikuppgifter med lösningar
Hämtad från ”https://wikiskola.se/index.php?title=Statistik_2C&oldid=43748”