(8 mellanliggande sidversioner av 2 användare visas inte) Rad 1:
Rad 1: === Konjugatregeln ===
=== Konjugatregeln ===
{{lm2c|Konjugatregeln|22-24}}
Så här ser den ut:
: Så här ser den ut:
a<sup>2</sup>-b<sup>2</sup> = (a-b)(a+b)
utför multiplikationen:
(a - b)(a + b) = a<sup>2</sup> + ab - ba - b<sup>2</sup>
vi kan stryka ab - ba = ab - ab = 0:
(a - b)(a + b) = a<sup>2</sup> - b<sup>2</sup>
V.S.B.
=== Konjugatregeln med <math> <math>\LaTeX</math> </math> ===
: a<sup>2</sup>-b<sup>2</sup> = (a-b)(a+b)
: <math> (a-b) \cdot(a+b) </math>
Så här ser ''beviset'' ut med LaTeX:
: <math>= a^2 +a\cdot b -a\cdot b -b^2 </math>
:
: vi kan stryka ab - ba = ab - ab = 0:
<math> (a-b)\cdot(a+b) </math>
<math>= a^2 +a\cdot b -a\cdot b -b^2 </math>
<math>= a^2-b^2 </math>
<math>\blacksquare</math>
Tips ( skriv såhär i Wikitexten och googla typsättning med TeX för råd ):
: < math> = a^2-b^2 < /math>
<math>(a-b)\cdot(a+b)</math>
<math> = a^2 +a\cdot b -a\cdot b -b^2 </math>
<math> = a^2-b^2 </math>
<math> \blacksquare </math>
: V.S.B.
=== Film ===
=== Film ===
Rad 68:
Rad 46: <math>(a - b)\cdot(a + b) = a^2 - b^2 </math>
<math>(a - b)\cdot(a + b) = a^2 - b^2 </math>
<ggb_applet width="962" height="463" version="4.0" ggbBase64="UEsDBBQACAgIACeiY0IAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAnomNCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1c23LbNhq+bp8Cw53JNLsRjRNPidyOkzpOZpO2U2c7O3sHiZDEiCK1JGXLmTzHPkH3vu1FHyC57zPtD4CUSB1sSZZreZNIIEic/u8/4ieU9jfTUYwuZJZHaXJsERtbSCbdNIyS/rE1KXot3/rm6y/bfZn2ZScTqJdmI1EcW9ym1rwf1GzKVOcoPLZ6vZCKkPmtnhBui3sObQlMwxYhQUi8gElHQmc0zaOnSfqdGMl8LLryvDuQI/Em7YpCjzkoivHTo6PLy0u7mt1Os/5Rv9+xp3loIVh5kh9b5cVTGK7R6ZLp5hRjcvTPt2/M8K0oyQuRdKWFFFWT6Osvv2hfRkmYXqLLKCwGgIEbuBYayKg/ADoJZlA7Us3GQO1YdovoQubQuVbVVBejsaWbiUQ9/8JcoXhGkIXC6CIKZXZsYZsAEJQ71GeY+L7rWyjNIpkUZVtSznlUjda+iOSlGVZd6Rk5DjxgQpRHnVgC7CLOga4o6WWAKSwom0A1L65i2RFZVZ+vhzyBv9Ag+iDVWMA8AwRUAvyEcvLEw/iJw3yzlvrEFirSNNajYuQE6ONHRDHF6IkqiCkoFK5rHmFzDzNTUFNwUzimDTfduWnKTRtu2nB2DZ1lfU5oeaNBaUUnq9NJgD71ceGjAVig06/RSRQRHxFRq9cFQ2rdRK9fFbysuqbq6YJgU5Dyoa++NF7uLSliO1FEarMaedhm0mpKwl2++Zx0izkXZXRGJV1FJXXWUHlLcGd0OrVJYS79T3+WpmR0mymXVHGHGRULdtf9HSb0cEPtK503JSnL62DY26LaR5U1bJcLQvlAtS3Fq5CjXC2RBdo4IYIcUF7XA1viIBJA4Sklpog4iDtQJT5yVekhpvSWI4Z8pNoRhrQJcnz44lqnXeTAWOqmZ5QbMY4chog2XBwBCkgbP8CEMmjhOMiBTmp2oqZlLuIuVJiPOCxQmT1PmRYG/aAOk1PECGKqL/EQdZFLkadMJ+HKorq+WjsMSpGLkau6gu0Eu2lsJvTwEVPUgBaM0zyagTuQ8XjGFY1jlIwnRYldeb87Cisci3SheZh2h88XwJYiL6praAQea+4XjQdruM0v2rHoyBjCi3MlBwhdiFipuR6/lyYFqmSAmnv9TIwHUTc/l0UBvXL0XlyIN6KQ05fQOq8WqKfW/rwtJ904CiOR/ARCooZQA6KZe9e2q3LvAQ7MNN00zcLzqxxEB03/JbMUTI5vB/U/joWuzBMeuM1HMGLeFUrmedB84gMTrtY888zU8mJGm5jKGUWon+lgal55nT9P4/mtcRolxQsxLiaZjtbAVmaKqpOkH0uNruY6xD3dYSednhtYmRnr3dUYatisoNN/kcZphkAnqQNk9suyY0rdRi1t1grrNli3wBWfonD2nARUt9Blx5S6FTDeLK0klVRkElxNE+Xa2sDgDbnUYqOCqEkSFW+qShF1h3NSVYfvJqMOSFxNLmqDkr0N2j5aELO2iHWMWgmdmEyjOBLZVV1bdMdGw/ZQZomMjQgmIAWTdJIbpagRMMnlD6IYnCThj7IP6vyDUBa1gCWZptXgoKKyG42go7lfoi6URPwDSDR3Q9nPZAWNWYzhiX6K6wqxdFsP9TJLR6+Ti3cgbgtLbR9V9LTzbhaNlVijDpj4oZwLbhjlAhxEWO8HxOdARVcZK2BAocAfpsn7SV8UmezLOLGQmBSDFKTr1P47DAImAGQevRUAAsUg1zqUT7NhPpCyeCenBRKd9AIafSVancdfib91HqNjJD79hlqo8+k3EEwZK858/s9FAssEu/b00V8Ifqa/ZA/QRSEopkCw/QCwsygfCugD7g0NRQJuDmWffx4mYt6JPAbvEjA0VWGtB5N9o2/Tx+jN599zNP30WyuAuxj1Pv8OeiJlHAt08fnnLJQJGn/+L5ra88FWfZ3/dPIjeorMZI2ZOMIY609LeZVj8GBgYVDgEA2vjOUIdheo0GqvLcdM+k80ckpKUdp5D5Z65pnN85ocwvOVNkBbCxGPB0LtbUpRicUVQFiXQz3g2zRcFCmQWM13sL5jo3NjKY26mgXDxRiG02authwto4Cr2rgysMFXMJPtgsX9YLayZtumiFXGz0zq1O/OxZuWSm1wugGx5/8HiDm2QzVizN4PYN10NBJJiBId6/2Qxlf9NLHmUYbAStSQIAo/JKjaRhqIJkX1vOxFTDNhmnWgYMdWFwoOxgsK59h6AYV7bH1rVlHOvYJtZhUVY2bjN31RAQHGEPbZud6sFKVr1BevohCUU+F5tBPPK39a+co5z+kSz8l6nq+XzFz2VW22DrGbbK5f57Js4utkcy5hLWwHRim5TXwtY63A9p2A1MKjxbBgc1aA2MRKvl8nyg9K7TmWPedQyrGKdb5P3mUiyVX6qukyN0e2c8/IziOKBZ9fgxyQ9hrhp8ZfcYItxrLADura3PGceWvnAbGjewM75vjsgxvf93q5LDTGBtPVBpptzKpFluiNwmoOftB7EUocUrt734wCWmDroXyQvi22Y154X8wjxum1nFuyb5FNgR52iancmD3fJpjM9SzgB8c+FRNvEwK9WGZgc0+1moMq0d03RccUd2gNue0YXfVsb4VOrQt42OqA5wY/3ITn2wcAD7Y5rv8hngbLtf2mr9gLWIvRoQKrGRuKpWjw9Kbgro746R5icszvNyYHgWXcgT2b63CHE+KXATrzfA7s8Zmr3xV5f1q8frpZvE5NM2ma9Uy83jfx+sDE6y9NvH62U7xO/7x4fb083FG8LnfyhNuI7Wo7wVaE6xRijMCnxGU+IYxwWjk13+GY+yCb3PF95UKVU6M2o5wyh3JwaASuD86r3eDRFlnRu19WbBLfL/HCqwL8Ju+oZyJ816bMA6NBXcd1wbgspWEfGIv6d2/lb+9WF9SoiuwXeYeZZhGYd86ZyzzssQDCxPsP7Tdnx+AhsGPZel2t4ZKyag5stDwMTzA8c1zOD3lP3AyBXj6AoBPgDerBjFcmiJwGk+idB+hnDwArbjNCg8ANeIA9gM11SrDAWvjYBfyIy0tDv9/4/LzU82Y0WGZvz5bCwOj6qG7RakQ3Yb+B2dhPhpLYHq5Byct8GbUDrwH8zDa41MEeGGmXBAyi8oMyDU0Wvo3C8Ypd1pnh4ckSD19ts9l6dd/aM+chtSG4AcYB9xwGF6zcMzmEBJgxHIAdZ3eiJG+jLEuz1TumV0v4vt4G39e74UuoyY/pcoOXTBtCTGzYitY3oNV7I95wrPwOjLZ+3Tyj+o9fNS7QcVJ1r2bLY3WyEo2iRGvcSEzV4Y6/fvoFAOjkaTwp5Hk3kzKZHzA1kcrsWAhXx1cVtVhfqUyIvuhFUzk7EjNIs+hDmhRNk73bloHgZVNGNuQR2cHyVIcBsm6NK2uyF4ArUQpFA6qyzhwunOWEBl6V0FivMD+mhSjkgsK8NgrTAt7q7MHzZc15JMZp/mwr/Sm73N7PPEQV2gD1sxtRP9se9bPDQP2gI6uV3Di5kRsn23Pj5DC40Tij0UwsB5ud2Ngj0Kc3An26PdCnhwb0XtLIuyb2V6aRS4TM9mFWoXNDrTPGNSFflWVmZZa53r9f7x/NKhwih80YuTLfzA7ifIizDf+3SDivE9d7PCayKkOznI8uUzQPKkOzlMDcCP39vv6+JumPba8ZlxhH2GI2CRompPSF2PY5JQyQ5xy2VtS9d+i3f5G9lI64B5bUTiTwm4+T7J7NJHaAAz9gHmMQ5NBgl33DIeX/xa187d1Yr5UatEaBWp7yzYEKLjF2fNe7/xcyO74TPikduHG9yznBsjM3rd+b1kPTOjYuerSTc+brnTPbg3PupkkYmZ0wNP++bP3Hr+hRv3iG8Kdf1otV/TcTc9EKlkRrL++N399SB1YvdlkPrlnsLRzJohpcZ5du4Oqf7sKHh4X8xvETxdW5p6ZPuM4EHRr28cFhv5X13yp+OjTsR4eF/Z2+2L0H7KfjDKZWjqeEU/2EiVgIHhxbj/49SYtnJqdxlKUwqzC39DBNvhXQz2oOstNeb/PXbdcejMsLkRX6wB8qs0C0furQcC2weeMuq+cm6jAd1X8opn/zWf7fEF//D1BLBwgKNUdU9AsAAMtCAABQSwECFAAUAAgICAAnomNCRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIACeiY0IKNUdU9AsAAMtCAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAjAwAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
<html>
<iframe scrolling ="no " src ="https: //tube.geogebra.org /material /iframe /id /390017 /width /1188 /height /912 /border /888888 /rc /false /ai /false /sdz /true /smb /false /stb /false /stbh /true /ld /false /sri /true /at /auto " width ="1188px " height ="912px " style ="border:0px; "> </iframe>
< /html >
[http://www.geogebratube.org/material/show/id/390017 Länk till filen]
=== Uppgifter ===
=== Uppgifter ===
Rad 77:
Rad 59:
2. Lös <math>x^2-1=0</math> för alla reella x.
2. Lös <math>x^2-1=0</math> för alla reella x.
''Tips : Använd konjugatregeln och nollregeln för ekvationen.''
{{khanruta|'''Khan: Parentesmultiplikation'''
{{khanruta|'''Khan: Parentesmultiplikation'''
Konjugatregeln
Ma2C: Konjugatregeln, sidan
22-24
Så här ser den ut: a2 -b2 = (a-b)(a+b) [math]\displaystyle{ (a-b)\cdot(a+b) }[/math] [math]\displaystyle{ = a^2 +a\cdot b -a\cdot b -b^2 }[/math] vi kan stryka ab - ba = ab - ab = 0: [math]\displaystyle{ = a^2-b^2 }[/math] V.S.B. Film Bondestam (tv) respektive Matteboken (th) förklarar:
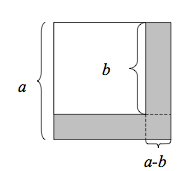
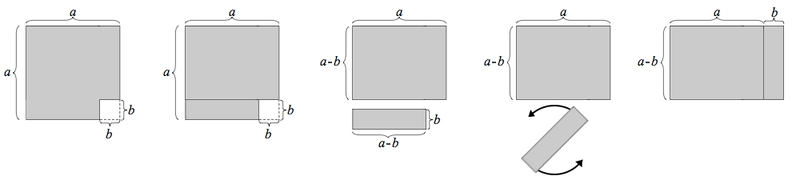
Geometriskt bevis av konjugatregeln Första beviset
Andra beviset
Visualisering
Här gäller:
[math]\displaystyle{ (x-y)\cdot(x+y) = x^2 - y^2 }[/math]
Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit.
[math]\displaystyle{ (a - b)\cdot(a + b) = a^2 - b^2 }[/math]
Länk till filen
Uppgifter Övningar (utan räknare)
1. [math]\displaystyle{ 1992\cdot 2008 = ? }[/math]
2. Lös [math]\displaystyle{ x^2-1=0 }[/math] för alla reella x.
Tips : Använd konjugatregeln och nollregeln för ekvationen.
Öva på Khan: Khan: Parentesmultiplikation
Hunnet så här långt kan vi repetera genom att lösa lite uppgifter på Khan Academy. De är dels av typen (a+b)(c+d) men också sådana som tillämpar kvadreringsregeln.
Khan om hur man multiplicerar binom ska du verkligen öva på.
Webbmatte