Fysik A Optik: Skillnad mellan sidversioner

VisuellWikitext

Nuvarande version från 15 juni 2012 kl. 22.09

Diverse

Många av texterna nedan har hämtats från Wikibooks om Fysik: Optik

Kursnavet

Optik på Kursnavet

GeoGebra-länkar

Du behöver ladda ner GeoGebra för att använda dessa:

Hur gör man? - Wikimarkup

Vi var två personer som arbetade fram detta material från grunden och det kan vara lämpligt med en introduktion om hur man skriver på wikin: Kort om Wikimarkup

Länkar

http://sv.wikipedia.org/wiki/Ljus

Vad är ljus?, s 189-197

Ljuskällor

Föremål som sänder ut ljus kallas för ljuskällor. Exempel på ljuskällor är solen, stjärnorna, glödlampor och datorskärmar.

Vi ska här använda strålar som en modell för ljus. I verkligheten består inte ljuset av strålar, men det är mycket praktiskt att använda denna modell för att förstå hur t.ex. kikare och speglar fungerar. Vi nöjer alltså med denna förenklade modell av ljuset för tillfället.

En ljuskälla är också materia och varje punkt på ljuskällan sänder ut ljus åt olika håll. Detta att ljuset sprider sig kallas divergens, man säger att ljuskällans alla ljusstrålar är divergenta ljusknippen.

Solen är vår viktigaste ljuskälla och vi befinner oss mycket långt från den. De ljusknippen solen sänder ut divergerar precis som vilken lampa som helst. Men p.g.a. av jordens litenhet och det stora avståndet blir divergensen mellan solens strålar som träffar oss mycket liten. Man brukar därför betrakta dessa strålknippen som parallella. Man kan också åstadkomma parallella strålknippen med hjälp av speglar och linser.

Med speglar och linser kan man också få strålknippen att falla in mot en gemensam punkt. De kallas då konvergenta.

Med speglar och linser kan man omvandla de olika typerna av strålknippen till varandra. Det är detta som görs i t.ex. en kamera och ett mikroskop.

ljusets hastighet

Ljusets hastighet i vakuum, c, är en fysikalisk konstant och är 299 792 458 m/s. Denna hastighet är oberoende av observatörens rörelse – två olika observatörer kommer alltid att uppmäta samma hastighet, oavsett hur de rör sig i förhållande till varandra. Som en mera åskådlig föreställning om ljushastighetens värde kan nämnas att hastigheten motsvarar sträckan jorden runt sju och en halv gång på en sekund.

Texten i ovanstående avsnitt kommer från Wikipedia.se

ljusstrålars utbredning

Kärnskugga och halvskugga

En skugga kan ses som bestående av två delar, kärnskuggan och halvskuggan. Detta gäller under förutsättning att ljuskällan som skapar skuggan inte är punktformig, utan har en synlig utsträckning, sedd från den plats där skuggan faller. Perfekt punktformiga ljuskällor finns egentligen inte i sinnevärlden, men stjärnor brukar betraktas som sådana, eftersom det ända tills helt nyligen har varit omöjligt att från jorden urskilja att en stjärna har en utsträckning. Fr Wikipedia

reflektion

När ljuset träffar på materia studsar ljuset mot föremålet och byter riktning - det reflekteras. Det är genom ljusets reflexioner som vi kan se de föremål omkring oss som inte sänder ut något eget ljus.

Det kan tyckas så självklart att det inte behöver någon närmare undersökning. Låt oss ändå titta närmare på detta. Om man riktar en strimma ljus mot en vit vägg ser man en ljus prick på väggen. Om man istället riktar ljuset mot en ren spegelyta ser man däremot ingen ljusprick. Orsaken till detta beror på hur ljuset reflekteras mot ytan. Mot den vita väggen sker en diffus reflexion men mot spegeln sker en regelbunden reflexion.

Regelbunden reflektion

Ljuset träffar en plan yta i en punkt. Den linje som går rätt ut från ytan i den punkten kallas för punktens normal. Ljuset bryts mot ytan så att dess infallsvinkel gentemot normalen blir lika stor som dess reflexionsvinkel. Detta kan vi formulera som en fysikalisk lag. Om vi döper infallsvinkeln till i och reflexionsvinkeln till r får vi sambandet:

i = r

Vi kan kontrollera att verkligheten verkligen följer detta samband i ett experiment. Genom att undersöka vilka infallsvinklar som ger vilka reflexionsvinklar kan vi konstatera att sambandet verkligen stämmer. Åtminstone för ljusreflexioner i speglar.

Diffus reflektion

Till skillnad från en spegel utgör en vit vägg inte en helt plan yta. Den består av små ojämnheter. När vi riktar vårt ljus mot väggen bryts dess strålar mot den skrovliga ytan och reflekteras åt olika håll. Man kan betrakta den vita väggen som en mängd pyttesmå plan, som var och en reflekterar ljuset åt olika håll. Det är detta som gör att vi kan se den ljusa punkten från olika håll. När ljuset träffade spegeln bröts ljusets strålar åt endast ett håll och blev därför bara synligt från ett håll.

Avbildning i plan spegel

I en spegel reflekteras ljuset så regelbundet att vi ser en bild av de föremål som ljuset kommer ifrån. Reflexionen i en spegel följer samma fysikaliska lag som reflexioner på andra ytor. Man kan använda detta faktum till att göra en konstruktion som visar hur en spegelbild uppkommer.

Buktiga speglar

Konkava speglar

Länkar

Konkava sfäriska speglar på Kursnavet

Uppgift

http://commons.wikimedia.org/wiki/Concave_mirror innehållermedia om fyra fall av avbildning med konkava speglar. Det finns texter att klippa in i respektive bild. Bilderna ska in här men bör även läggas in på sv och eng wikipedia. Bildtexterna på wikimedia bör översättas till svenska

Praktisk övning

Praktisk övning i att rita strålar vid reflektion i en konkav spegel. Vi använder förstorade papperskopior på övningen i boken. linjal behövs.

Konvexa speglar

Förstoring

Ljusets brytning, s198-203

Ljusets brytning

Ljuset reflekteras i samma vinkel och bryts in mot normalen.

Snells lag

Snells lag är den enkla formeln som används för att beräkna vinklarna vid refraktion (ljusbrytning) då ljus färdas mellan två medier med olika brytningsindex. Den är uppkallad efter dess holländske upptäckare Willebrord Snell (1580-1626). fr Wikipedia

Minnesregel

En bra minnesregel för att bestämma ljusbrytningens riktning är det faktum att ljusstrålen i det tätare mediet alltid befinner sig närmare normalen. Ett praktiskt sätt att komma ihåg detta är att tänka sig ljusstrålen som en bil som kör från en asfalterad yta (det tunnare mediet) och in på lerigt underlag (det tätare mediet). Beroende på vinkeln kommer då antingen det högra eller det vänstra hjulet att passera gränsen först vilket gör att bilen svänger. fr Wikipedia

Snells lag

n₁*sin θ₁ = n₂*sin θ₂

Läs mer

Läs om Snells lag på eng WP.

Totalreflektion

När en ljusstråle färdas från ett tätare medium till ett tunnare (dvs n₁ > n₂) kan man lätt konstatera att ekvationen saknar lösning då θ₁ överstiger ett visst kritiskt värde kallat gränsvinkeln θ_g. Detta beroende på att sin(θ₁) alltid är mindre än (eller lika med) 1.

[math]\displaystyle{ \theta_{g} = \arcsin\left( \frac{n_2}{n_1} \right) }[/math]

Då θ₁ > θ_g lyckas inget ljus passera gränsytan och totalreflexion inträffar, dvs. allt infallande ljus återspeglas. Detta kan till exempel inträffa när ljus färdas från vatten till luft, eftersom vatten är ett optiskt tätare medium än luft (n_vatten > n_luft), om infallsvinkeln samtidigt överstiger θ_g.

Texten i ovanstående avsnitt kommer från Wikipedia.se

Brytningsindex

Brytningsindex är ljusets hastighet i materialet dividerat med ljushastigheten i vakuum.

[math]\displaystyle{  n = \frac{c}{b} }[/math]

där n är brytningsindex, c är ljushastigheten i vakuum och v är ljushastigheten i materialet.

Reflektion, brytning och totalreflektion

GeoGebra. Ljusets brytning när det går från ett material till ett annat. Snells lag. Du kan använda glidarna för att variera brytningsindex i första och andra materialet.

<ggb_applet width="1093" height="601" version="4.0" ggbBase64="UEsDBBQACAAIAHx0lEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAB8dJRAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1d65LbxrH+7TzFFE8dlWSLXMwVA2vXKckXWYluJSmpnJNyVCCJ5cJLAgyAXe268sM/8ybn7zmJ/QJ5APsd8iSnZwYgcSMJcknukpTLWhDAYGa6v+6e7sZg5vi3V6MhuvSi2A+DkxbuWC3kBb2w7weDk9ZFctqWrd9+8ZvjgRcOvG7kotMwGrnJSYupkn7/pMVtWzKrx9unTt9pM8JZ22Vdt83tUyyxwy1XOi2ErmL/8yB86Y68eOz2vLe9M2/kPg97bqIbPkuS8edHRx8+fOhkTXXCaHA0GHQ7V3G/haCbQXzSSn98DtUVHvpAdXFiWfjoTy+em+rbfhAnbtDzWkiRcOF/8ZtPjj/4QT/8gD74/eQMCMYWbqEzzx+cAVE2FS10pEqNgSNjr5f4l14Mz+ZONdHJaNzSxdxA3f/E/ELDCT0t1Pcv/b4XnbSsDiXAFktIjB3p6AbDyPeCJC2L0zaPstqOL33vg6lW/dItshZKwnDYdVWN6G9/Q8QiFnqoDtgcCByEMLcsc82i5kDMgZkDN2WYeZyZosyUYaYMoy106cd+d+idtE7dYQws9IPTCOCbnMfJ9dDT/UkvTKnHD4Gm2P8BClML5MTwHK5b1kP1T8A/pm4cFYnEuVaT6GLJRrMmseXQ5m2SG1FKJ3Ryu9omoF5Pp5jTqCG8EaE8x1toSv+v/1VapPPILLdozm/WoGBbIfH4KNOV41Q9UHymyqbik3ijWCkMdRB3lNxjxEE5hA1izhF24GATBOqAMEeMwymWSKijjagNNxiiSCJVDlOktYNL+MNsXZlAHCpTV21QSoShIYY4RVgrFUOgSkgrJigpoVCCc8ThIdU8JqoKKhATcEYlYtBHpZM2hoIUHoRzaJ4gihFVD2MbEYGEqg8zpetCqq5DlQQJCwmsKgS1BpU26gzlJaKKmsyu+cH4IimwqDfqZz+TcDzBAkqDQZqaPWOgClbxk+Oh2/WGMFK8VUgidOkOlUbohk7DIEEZiMRcG0Tu+MzvxW+9JIGnYvS9e+k+dxPv6hsoHWdt67K9MIhfR2HyZTi8GAUxQr1waE36HA5x7jeZ9BpOaO4Gy9/guRsi99uubTeEO+gi9qD9MIqz4m6//0yVmJoG4OSrYHj9JPLc83HoF8k4PtKDzrF30Rv6fd8N/gjCqlpRfEGTMUjbq2wM4jbNehJG/bfXMYgwuvpvLwpBqRzekY6QhDnEsWwbdOza3KGYd2xBbUsSGHMpFwB43HOV8kkYqoXNKCUW57YFhuC6/g4z7XqXE3zcK29K6iBSep07eRY/CYfTS5r6L91xchFp5wFoihRJj4PB0NMSovUaRubeeTe8emtEg5q63l2P4cwyPegONNcRWAbCORRIj11z1GVU1yalLF3G0iWsTNb8/rQWoE3Xoo5dc9SlQHhN11JScUYmsbJm/FjbM6uVak1mq5Toq3H+IvCT59lJ4vfOp6SqB15ejLreRICKdeL11al6DS5HnPwpdeLU7//K/X535iWuckY4odyRts3hL3GkNHJaktDjcy8KvGGqECAMF+FFbPQ7pyt9r+eP4NTcSJXcVXD/AQgwV/veIPIywofasTMM13dxXtSnl61cVd9E4ehZcPkOZKnUgeOjrJfHcS/yx0pmURcGkXNvKpVAuwtjUD//nNJgYF1PjTXA3kSxFnT7IjkLI+26gUmCo1LcoTcCRw0lWjyDi5EX+b0JUONEO4HQq4u0447VYdxhwhYOloTQVMwUaCjsfg+mswx2jp1QYIZEI3c4PtPopQwbutdeVOCVru5F2C8y1g0AIE0mmJGxEaCx5xnZS1KdQ2OoTqtsjrUp5Qt5EOAyD5TIValOfQrz0FRuV6OZzKM5Hiq/G41840eM3Ctti9xuDENJApEHyGMwjTxMxyam2FIKo57AOsK5hsYEV79O/StvMlKCoPg/gGK4BWKm1iSBYe4cnPlY+5cTRqsf3/r9vhfMRAjabwoSaP2gayQfoTD4w9jILVjvPyo0/jxOHj47/bOL7w2SR7/+eISl9fD+eJx8Ng6SB0dEOajt+/fvB6Qd4AdHcPwMjg/+Qj6FGw++++7ef2Drkf5TqhBK3hsmj6DwPXc0fqT/3DetnLixH8D9I1XTw0JzcypMn5VOx/k07af1cJx8992Skkiqksj3QRItkkoixBgfJfEOSqIepyYi5dZZRAj+GcQyhICrBaNuVT6sT//1v6mIOOZ3IzGxSSolQqZCIptaq9WUAlurqwWZuA1hZCTN8E/cQGijnnIk09DDmiXJWHO0LMv4oywrWb4aR8Bqxa5MgoHpcBV+6IYx+hSpHy5+gI5QQB6Y6HC+NXYr1tjqCEKl4zDHoZQzyZ0lDe/8TvcnnSbQXyAX+vrrj0262q90lUIwxYS0JOaEMMmyoGNNXYWAN8Fpb+/99SJMHpm/6DPUJ/Anf62OAPV8q1jZer1Mq6LQ9V5m5uhB97Qz/Xg4DD94/UqgECdulLxW8SFStop1hNS2inXAFKIfJj7jAraNU56RTCDJA/jVC+NUNO8bKQUO5u+gtjptJLTJuE5opWUxQiQTXHJ7zZIQLCApT1EjCoIqBVxAbC8tYXEmhJOFvmuiAGxRSgIYOOh6Mv7LfU1DQDJCiMZGm5GUsEakjGvCK6cjBBU2OEKYQPRK10tKUCIlWBspQYUUiTuEcyKwxIQKbNtrRiXKkdJGGqUmLI+q4kOpoEQwIm1sWzYha+Z5qaNBs44GlY5iCTab2VRiaQsqJ7H3ujpa6mezblZ66XQ4szglFMYW2xZi7eMKLYwrSYBO0GRwgbNscEHaZUjGhdvj0m2Qmvx9dTopkJYIiiWCaYm0hqhYQ1S6HxTvB+X7xerLtRcfjlYZOuluDZ1t0hFW4T9uQsOOLQuXycxxtcAPnbSd0PpkETMWh8s6UbsqNxqkq2b47Av5qFOMsWKhlQZKQh1/yOWrNC9y0UT+aik3mWdoLxyN3KCPAv1qS0PVmr5qca2T1tXjKz9O2XaRZFe/NBWljy9A5svVkMHEpM/1cSfQyXId1prQmcfUrw9J3MkWGPrNITG0vS6OFg3IW2+grpdMyNfAFKwYXLYi3flWJE5rywDoVhEqpH5mjHaYU2NH1LGbHjc25rkXV/7Qd6Nrc2cqNFMQWMlMtKe9mJtFwvVpJO+vgXkmNi/a/NF46Pf8ZMLuoZKYZ0HiRbHpe/Vt2LnnjdVrzFfBu8gNYjVRqtj/plr0+FBsvbVmW19UpDdh4iZeSY+eGD1yofMuUawu69OTe+44jB8tMzZnj9yu7VuC720OsaeatWdJiwiKJU1HCOlYnKhJYAJbxMFbs24ZBzU2VUz6y9m4/mo2bk0efSW7zRri08Dq1SAEuNWgudgisvl59a0bxCa6m5eStk7s0Y56reKo/NisVPUMNX+zlIa/2R3lph0OIkIdwQiWtoOJcVZYRwpHEEcK2+EWtekGlPuFH0VhNA+17ix7u7LV3TXb29D0bgIePRGr3q98bPQkN/gVQPrl/+YjU3wBCqXLublZL0A3+AqS5gB7dXoae4nJnzCjD9SpBXTTryhZ5l8pQXnjnQ69Kw1L2eYvkKjlQC6qSh7wr6tQ/2MpqP+xTqh7YdD3jdOpplWmhWvkIJvPZ+QAq2TX0pJAUzmwl5IDe5fl4Juisr+pgv/PpcD/Z+0rXsciGHAnnMBIUwP+LMtcj/5wlhXguCYSbWwGQP213WX7aQWaZyG/WmbM/WqBZ70vgWkbi42Gps3heboMPE8PBJ61ozOPqd+uxNRdSGk2CDgnnG7LLbD62SGzur1+XpeNzvB6EAYls/OV8QmeGp/gWzhQBUTZDo3hYWyK9t+nybOBKXwGB3bS8hdZKtP65NW4rnDmaGrNH01vnMAuCoo2ff1r4JPf019sisnpoHja1TKQnsCz91UWItDTQpj+miiM3qrvW3Oittmk+GzdqqTF3tdME7s5724h+Z/ljSlplv1fIEy3nPwv4zTYE5RkaZBuYyL3CKazPYFp8jpzqk2Eiz0Cyt8ToNp7plBF3+93h+77SYKptB1JBLepSVI6HekQGzPsOLZDCSUb98B/f8goYN7BthSYWBgQIEKQDaKwhG/+O+Nu/964209rfXOS+ebEFP7eFD43vvngPV7eOyezvfMFua6129qb+OZ4N3xzsuI81Ls3TNXoy7V20QsWjmavqTGXHSJB32zsCOFgO/t2bAXBu2Oex/f7gmk14KIwYnEhJGfUUViyyoIKO4va+b6gVq+IB6iHg7rMx25iWo3WGk58vCNANZkNNklJlh2d3nwnpgx7b2/ngS2bALtrUlD/6RIpfLpkXoiGp+hZ0POhtz0v/arnaPFHPTXO1HqRr/++PS2nv71f8lUuwF77ub/+6Icby40tOl+d3rjXJVV6bFSpMsmqoFbufLWKoNbJV93NGdt4Msdsrufc/nECXrye+DP1/SvXuvlrN/D3V1bdnBdcN6Nr5lzNnZ6qOVPoqvNLTptL2ulNJW3mxJFFkhbVSFr5Wjd/7XYlrWZi53XtLNDdmxM8L1P1fH8/NWoSZPMtzoB4cdispltk9cuPrNbRDd4Cr18dNq/5Nnn9fHEEfhjc3gazXxw6s+kWmf3yI7O3Nzy+OnRmr9vta/IW8vn7dOLfi2zi30v9gxo8yjGeenVIs0eG2SOj7JFA/2AnrXCVd5L0/Zw5gwvCl6XTQdna03UfveMawcHzBGeJqfzzs5rDVafxNc9u0RsQslT+cjrjaIfj0jJAo80DNDf9uJapECU7Q/cIn2AP8KmsQbLLiZ0yQOEeANQua5AeuncVoXIwt3Cyyn57YbQjOZEEC6KXGrSkSEczW0jbppJYnDrM2fx0vReHjgS+K0i8/IhELRK4hASWWwgSDxyKGeZpU1BU3uU/f58tQvqqVUToaOHIsnA5zruzkscGMqgVVr6YsPLlkqx8sVOs3Gri/+Wts+bWDcQ2U3YHzuzbSdnRLGVHs5QdzVJ22aLp5ZQdzVJ2NEvZ0SxlR7OUHV0lZUc/puxqdGDHU3b7lbHbOD63kHDYr5zd7iO05zm73QeorEH7lLFjh+2EyY5FuZAcwmFMMZEsnSRpMZtDgMwtybCN2RYSdgcOhCgBIW4JiJcfgagDgmwdiFeHDkS9adoMEM1iR5bFjiyLHVkWO2Z7KpVjR5LFjiSLHUkWO5IsdiSrxI5zPkI/lNhx4x8zbS12xB2n8J9Mv0oAW+RwLLBtYaG+QN1Zr6saWN7ul2ib8IrLA8e8FXF3C61gD9CaBJkzdI2VVI3uDXrhHqBXTeJUvYNdxasckfKDd/vWu4vU/LBzy9yerrRtG3f2DiNBtonEy0OX+wm36VZePh44t+W6ud0sguRZBMmzCJJnEWS2f3Y5gmRZBMmyCJJlESTLIki2SgTJPkaQNRmWHY0gJ3u27tfrx40DtPUocZ/wCfYAn0lcmGlQG89fO3a3IAr3AKLa4G9nEeqG4dBzp4OxV94rKLc00g2Wm20+Lk1DEmFS7JyIeZD2zrzeeTe8Qno5pwJk7lh7dLr0W9V5vYVPLwHc1Wo4S/FleIf4YpaOUdPl18eXyF2NL6MyX/Ku8ZYZQ4idcqZ+u6gVODNZ3ewr79J3g15FmxYtsrRgy9RgvqucX2kpuOlKS6Mqx/WWbIP0WNmibd0O5EY2SJ1uGc3vhn1dvIVUUBGD14sipny0/Ho7+07PxXor+0fRDlYpVWyDNFjMZkxmOXObYYdizhzb4Y60t7QJ55M3hY35Xldg/OWn+TiW9uX7qbovH2OMUIeCbXc44Va2XO8NNuYboX///X/Q/V9+QveGySP064/oCJEHNUFxuldjZgryBrjxXo3GMVpus751bdXIM9Fc32Z99etfssL6l6+9qKcQhjHiuT84S5A2ESM/SdR4emIKoc/QOIE/5uw/0xUyaz4OqSyRuYS/XI9/eHsJgzhxo0QbQL08ZtvuONJiwmLUIRKkW2YrjquFqbnNmW0TZoniprrNXZHw7rhohMh1+66pnLkDL875scpgTQTO6zcTYD5fgKe1n6Cp+EYriW9NXnfPxNfqEMoth3JMCZbg0shZ0rt4gHm9cOPXn5caYH4uawTvSCodxh3wsySjVDRXj/mjy89bGF1IurxuvUptei/YDQwvRYF4B+py6nvDftlbJBUx0DefhFcLVuZJJjVmcE4f3HAWZoZ/QNJVT0X9bs7NnUur3rmsXdIZoD/3+k+90Fi9jJ9DLxgkZym4K0JTXVYp4/CCWXSzodnqNLIcNDjdaVne1O+/CTR4bdC4s6FZ8HHcbGi2+nXYFBrJjd3Dc99DbRYZtwYZVkYGWBrEUIU2f+p84IUDrxu5X/w/UEsHCG5PkwOJEgAAv64AAFBLAQIUABQACAAIAHx0lEBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAfHSUQG5PkwOJEgAAv64AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAhEwAAAAA=" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "false" allowRescaling = "true" />

Brytningsindex för några material

Vakuum	1 (exakt)
Syrgas	1,00027
Luft	1,00029
Kvävgas	1,00030
Vatten	1,33
Etanol	1,36
Bergkristall	1,46
Terpentin	1,47
Kronglas	1,51
Flintglas	1,75
Guanin	1,83
Diamant	2,47
Titandioxidkristall	3

Texten i ovanstående avsnitt kommer från Wikipedia.se

Färger, s 204-207

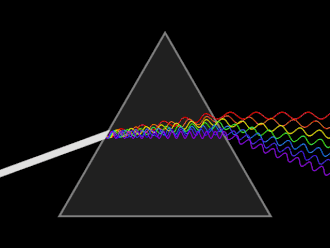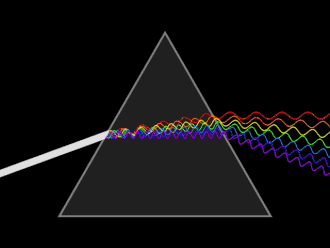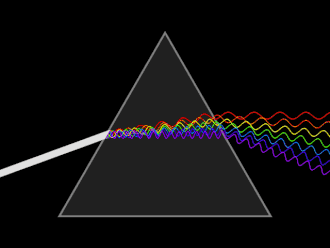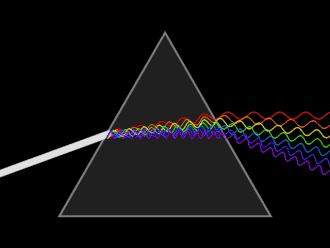
Komplementfärg kan man säga är en färgs motsatsfärg. I vissa färgcirklar ligger dessa färger mitt emot varandra. När man blandar dessa två motsatsfärger uppstår en neutraliserad ton (grå).

Ett objekt som diffusivt (spridande) reflekterar alla våglängder uppfattas som vit, medan ett objekt som absorberar alla våglängder uppfattas som svart. {{wp} Om föremålet absorberar en färg, exempelvis blå kommer det att uppfattas som att det har komplementfärgen, exempelvi orange.

Linser, s 208-211

Konvexa linser

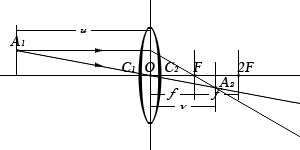
Konkava linser

Simulering av linser

Länkar

Linsens förstoring, s 212-215

Kameran och ögat, s 215-219

Optiska instrument, s 220-225

Optiska fibrer

Laboration optik

TEDT10 ni får göra laborationen på måndag morgon. Tyvärr har det dykt upp en konferens som jag måste närvara vid.

Materialet finns i lådorna.

Läs igenom hela instruktionen först.

Dela in er i lagom stora grupper och labba.

Var försiktiga, utrustningen är dyr.

Jag finns i salen bredvid om ni har några viktiga frågor.

Synfel

http://celebrate.ls.no/Norsk/Animasjoner/NMfag/linser_fokuseringsfeil.swf

repetition

Titta på provet med lösningar nedan.

@@ Rad 3: / Rad 3: @@
 Många av texterna nedan har hämtats från [http://sv.wikibooks.org/wiki/Fysik_A/Optik Wikibooks om Fysik: Optik]
+==== Kursnavet ====
+[http://kursnavet.se/kurser/fy1201/fy1201w/O_1_1_020_ljuset.htm Optik på Kursnavet]
 ==== GeoGebra-länkar ====
@@ Rad 12: / Rad 16: @@
 * [http://www.geogebratube.org/student/m4576 Concave convex mirrors]
-{{clear}}
+=== Hur gör man? - Wikimarkup ===
+Vi var två personer som arbetade fram detta material från grunden och det kan vara lämpligt med en introduktion om hur man skriver på wikin: [[Kort om Wikimarkup]]
 '''Länkar'''
 http://sv.wikipedia.org/wiki/Ljus
+{{clear}}
-== Hur gör man? - Wikimarkup ==
-[[Kort om Wikimarkup]]
 == Vad är ljus?, s 189-197 ==
@@ Rad 42: / Rad 45: @@
 === ljusets hastighet ===
+Ljusets hastighet i vakuum, c, är en fysikalisk konstant och är 299 792 458 m/s. Denna hastighet är oberoende av observatörens rörelse – två olika observatörer kommer alltid att uppmäta samma hastighet, oavsett hur de rör sig i förhållande till varandra. Som en mera åskådlig föreställning om ljushastighetens värde kan nämnas att hastigheten motsvarar sträckan jorden runt sju och en halv gång på en sekund.
+{{wp|http://sv.wikipedia.org/wiki/Ljusets_hastighet}}
 === ljusstrålars utbredning ===
@@ Rad 85: / Rad 91: @@
 === Konkava speglar ===
+[[Image:concavo_1.png|thumb|200px|Concave mirror (When the object is beyond the curvature's center (C) of the sphere, the image will be inverted and smaller than the object.)]]
+[[Image:concavo_2.png|thumb|210px|Concave mirror (When the object is located on the curvature's center, the image will be inverted, same size.)]]
+[[Image:concavo_3.png|thumb|200px|Concave mirror (When the object is located between the curvature's center and the focus (F), the image will be inverted and greater than the object.)]]
+[[Image:concavo_4.png|thumb|200px|Concave mirror (When the object is located between the focus and the vertex, the image will be virtual, upright and greater than the object.)]]
+==== Länkar ====
 [http://kursnavet.se/kurser/fy1201/fy1201w/O_1_2_070_konkava.htm Konkava sfäriska speglar på Kursnavet]
+==== Uppgift ====
+http://commons.wikimedia.org/wiki/Concave_mirror innehållermedia om fyra fall av avbildning med konkava speglar. Det finns texter att klippa in i respektive bild. Bilderna ska in här men bör även läggas in på sv och eng wikipedia. Bildtexterna på wikimedia bör översättas till svenska
+==== Praktisk övning ====
+Praktisk övning i att rita strålar vid reflektion i en konkav spegel. Vi använder förstorade papperskopior på övningen i boken. linjal behövs.
 === Konvexa speglar ===
@@ Rad 127: / Rad 147: @@
 :<math>\theta_{g} = \arcsin\left( \frac{n_2}{n_1} \right)</math>
-Då θ<sub>1</sub> &gt; θ<sub>g</sub> lyckas inget ljus passera gränsytan och [[totalreflexion]] inträffar, dvs. allt infallande ljus återspeglas. Detta kan till exempel inträffa när ljus färdas från vatten till luft, eftersom vatten är ett optiskt tätare medium än luft (''n''<sub>vatten</sub> > ''n''<sub>luft</sub>), om infallsvinkeln samtidigt överstiger θ<sub>g</sub>.
+Då θ<sub>1</sub> &gt; θ<sub>g</sub> lyckas inget ljus passera gränsytan och totalreflexion inträffar, dvs. allt infallande ljus återspeglas. Detta kan till exempel inträffa när ljus färdas från vatten till luft, eftersom vatten är ett optiskt tätare medium än luft (''n''<sub>vatten</sub> > ''n''<sub>luft</sub>), om infallsvinkeln samtidigt överstiger θ<sub>g</sub>.
 {{wp}}
@@ Rad 134: / Rad 154: @@
 Brytningsindex är ljusets hastighet i materialet dividerat med ljushastigheten i vakuum.
-  n = C/v
+  <math> n = \frac{c}{b}</math>
   där n är brytningsindex, c är ljushastigheten i vakuum och v är ljushastigheten i materialet.
@@ Rad 143: / Rad 163: @@
 <ggb_applet width="1093" height="601"  version="4.0" ggbBase64="UEsDBBQACAAIAHx0lEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAB8dJRAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1d65LbxrH+7TzFFE8dlWSLXMwVA2vXKckXWYluJSmpnJNyVCCJ5cJLAgyAXe268sM/8ybn7zmJ/QJ5APsd8iSnZwYgcSMJcknukpTLWhDAYGa6v+6e7sZg5vi3V6MhuvSi2A+DkxbuWC3kBb2w7weDk9ZFctqWrd9+8ZvjgRcOvG7kotMwGrnJSYupkn7/pMVtWzKrx9unTt9pM8JZ22Vdt83tUyyxwy1XOi2ErmL/8yB86Y68eOz2vLe9M2/kPg97bqIbPkuS8edHRx8+fOhkTXXCaHA0GHQ7V3G/haCbQXzSSn98DtUVHvpAdXFiWfjoTy+em+rbfhAnbtDzWkiRcOF/8ZtPjj/4QT/8gD74/eQMCMYWbqEzzx+cAVE2FS10pEqNgSNjr5f4l14Mz+ZONdHJaNzSxdxA3f/E/ELDCT0t1Pcv/b4XnbSsDiXAFktIjB3p6AbDyPeCJC2L0zaPstqOL33vg6lW/dItshZKwnDYdVWN6G9/Q8QiFnqoDtgcCByEMLcsc82i5kDMgZkDN2WYeZyZosyUYaYMoy106cd+d+idtE7dYQws9IPTCOCbnMfJ9dDT/UkvTKnHD4Gm2P8BClML5MTwHK5b1kP1T8A/pm4cFYnEuVaT6GLJRrMmseXQ5m2SG1FKJ3Ryu9omoF5Pp5jTqCG8EaE8x1toSv+v/1VapPPILLdozm/WoGBbIfH4KNOV41Q9UHymyqbik3ijWCkMdRB3lNxjxEE5hA1izhF24GATBOqAMEeMwymWSKijjagNNxiiSCJVDlOktYNL+MNsXZlAHCpTV21QSoShIYY4RVgrFUOgSkgrJigpoVCCc8ThIdU8JqoKKhATcEYlYtBHpZM2hoIUHoRzaJ4gihFVD2MbEYGEqg8zpetCqq5DlQQJCwmsKgS1BpU26gzlJaKKmsyu+cH4IimwqDfqZz+TcDzBAkqDQZqaPWOgClbxk+Oh2/WGMFK8VUgidOkOlUbohk7DIEEZiMRcG0Tu+MzvxW+9JIGnYvS9e+k+dxPv6hsoHWdt67K9MIhfR2HyZTi8GAUxQr1waE36HA5x7jeZ9BpOaO4Gy9/guRsi99uubTeEO+gi9qD9MIqz4m6//0yVmJoG4OSrYHj9JPLc83HoF8k4PtKDzrF30Rv6fd8N/gjCqlpRfEGTMUjbq2wM4jbNehJG/bfXMYgwuvpvLwpBqRzekY6QhDnEsWwbdOza3KGYd2xBbUsSGHMpFwB43HOV8kkYqoXNKCUW57YFhuC6/g4z7XqXE3zcK29K6iBSep07eRY/CYfTS5r6L91xchFp5wFoihRJj4PB0NMSovUaRubeeTe8emtEg5q63l2P4cwyPegONNcRWAbCORRIj11z1GVU1yalLF3G0iWsTNb8/rQWoE3Xoo5dc9SlQHhN11JScUYmsbJm/FjbM6uVak1mq5Toq3H+IvCT59lJ4vfOp6SqB15ejLreRICKdeL11al6DS5HnPwpdeLU7//K/X535iWuckY4odyRts3hL3GkNHJaktDjcy8KvGGqECAMF+FFbPQ7pyt9r+eP4NTcSJXcVXD/AQgwV/veIPIywofasTMM13dxXtSnl61cVd9E4ehZcPkOZKnUgeOjrJfHcS/yx0pmURcGkXNvKpVAuwtjUD//nNJgYF1PjTXA3kSxFnT7IjkLI+26gUmCo1LcoTcCRw0lWjyDi5EX+b0JUONEO4HQq4u0447VYdxhwhYOloTQVMwUaCjsfg+mswx2jp1QYIZEI3c4PtPopQwbutdeVOCVru5F2C8y1g0AIE0mmJGxEaCx5xnZS1KdQ2OoTqtsjrUp5Qt5EOAyD5TIValOfQrz0FRuV6OZzKM5Hiq/G41840eM3Ctti9xuDENJApEHyGMwjTxMxyam2FIKo57AOsK5hsYEV79O/StvMlKCoPg/gGK4BWKm1iSBYe4cnPlY+5cTRqsf3/r9vhfMRAjabwoSaP2gayQfoTD4w9jILVjvPyo0/jxOHj47/bOL7w2SR7/+eISl9fD+eJx8Ng6SB0dEOajt+/fvB6Qd4AdHcPwMjg/+Qj6FGw++++7ef2Drkf5TqhBK3hsmj6DwPXc0fqT/3DetnLixH8D9I1XTw0JzcypMn5VOx/k07af1cJx8992Skkiqksj3QRItkkoixBgfJfEOSqIepyYi5dZZRAj+GcQyhICrBaNuVT6sT//1v6mIOOZ3IzGxSSolQqZCIptaq9WUAlurqwWZuA1hZCTN8E/cQGijnnIk09DDmiXJWHO0LMv4oywrWb4aR8Bqxa5MgoHpcBV+6IYx+hSpHy5+gI5QQB6Y6HC+NXYr1tjqCEKl4zDHoZQzyZ0lDe/8TvcnnSbQXyAX+vrrj0262q90lUIwxYS0JOaEMMmyoGNNXYWAN8Fpb+/99SJMHpm/6DPUJ/Anf62OAPV8q1jZer1Mq6LQ9V5m5uhB97Qz/Xg4DD94/UqgECdulLxW8SFStop1hNS2inXAFKIfJj7jAraNU56RTCDJA/jVC+NUNO8bKQUO5u+gtjptJLTJuE5opWUxQiQTXHJ7zZIQLCApT1EjCoIqBVxAbC8tYXEmhJOFvmuiAGxRSgIYOOh6Mv7LfU1DQDJCiMZGm5GUsEakjGvCK6cjBBU2OEKYQPRK10tKUCIlWBspQYUUiTuEcyKwxIQKbNtrRiXKkdJGGqUmLI+q4kOpoEQwIm1sWzYha+Z5qaNBs44GlY5iCTab2VRiaQsqJ7H3ujpa6mezblZ66XQ4szglFMYW2xZi7eMKLYwrSYBO0GRwgbNscEHaZUjGhdvj0m2Qmvx9dTopkJYIiiWCaYm0hqhYQ1S6HxTvB+X7xerLtRcfjlYZOuluDZ1t0hFW4T9uQsOOLQuXycxxtcAPnbSd0PpkETMWh8s6UbsqNxqkq2b47Av5qFOMsWKhlQZKQh1/yOWrNC9y0UT+aik3mWdoLxyN3KCPAv1qS0PVmr5qca2T1tXjKz9O2XaRZFe/NBWljy9A5svVkMHEpM/1cSfQyXId1prQmcfUrw9J3MkWGPrNITG0vS6OFg3IW2+grpdMyNfAFKwYXLYi3flWJE5rywDoVhEqpH5mjHaYU2NH1LGbHjc25rkXV/7Qd6Nrc2cqNFMQWMlMtKe9mJtFwvVpJO+vgXkmNi/a/NF46Pf8ZMLuoZKYZ0HiRbHpe/Vt2LnnjdVrzFfBu8gNYjVRqtj/plr0+FBsvbVmW19UpDdh4iZeSY+eGD1yofMuUawu69OTe+44jB8tMzZnj9yu7VuC720OsaeatWdJiwiKJU1HCOlYnKhJYAJbxMFbs24ZBzU2VUz6y9m4/mo2bk0efSW7zRri08Dq1SAEuNWgudgisvl59a0bxCa6m5eStk7s0Y56reKo/NisVPUMNX+zlIa/2R3lph0OIkIdwQiWtoOJcVZYRwpHEEcK2+EWtekGlPuFH0VhNA+17ix7u7LV3TXb29D0bgIePRGr3q98bPQkN/gVQPrl/+YjU3wBCqXLublZL0A3+AqS5gB7dXoae4nJnzCjD9SpBXTTryhZ5l8pQXnjnQ69Kw1L2eYvkKjlQC6qSh7wr6tQ/2MpqP+xTqh7YdD3jdOpplWmhWvkIJvPZ+QAq2TX0pJAUzmwl5IDe5fl4Juisr+pgv/PpcD/Z+0rXsciGHAnnMBIUwP+LMtcj/5wlhXguCYSbWwGQP213WX7aQWaZyG/WmbM/WqBZ70vgWkbi42Gps3heboMPE8PBJ61ozOPqd+uxNRdSGk2CDgnnG7LLbD62SGzur1+XpeNzvB6EAYls/OV8QmeGp/gWzhQBUTZDo3hYWyK9t+nybOBKXwGB3bS8hdZKtP65NW4rnDmaGrNH01vnMAuCoo2ff1r4JPf019sisnpoHja1TKQnsCz91UWItDTQpj+miiM3qrvW3Oittmk+GzdqqTF3tdME7s5724h+Z/ljSlplv1fIEy3nPwv4zTYE5RkaZBuYyL3CKazPYFp8jpzqk2Eiz0Cyt8ToNp7plBF3+93h+77SYKptB1JBLepSVI6HekQGzPsOLZDCSUb98B/f8goYN7BthSYWBgQIEKQDaKwhG/+O+Nu/964209rfXOS+ebEFP7eFD43vvngPV7eOyezvfMFua6129qb+OZ4N3xzsuI81Ls3TNXoy7V20QsWjmavqTGXHSJB32zsCOFgO/t2bAXBu2Oex/f7gmk14KIwYnEhJGfUUViyyoIKO4va+b6gVq+IB6iHg7rMx25iWo3WGk58vCNANZkNNklJlh2d3nwnpgx7b2/ngS2bALtrUlD/6RIpfLpkXoiGp+hZ0POhtz0v/arnaPFHPTXO1HqRr/++PS2nv71f8lUuwF77ub/+6Icby40tOl+d3rjXJVV6bFSpMsmqoFbufLWKoNbJV93NGdt4Msdsrufc/nECXrye+DP1/SvXuvlrN/D3V1bdnBdcN6Nr5lzNnZ6qOVPoqvNLTptL2ulNJW3mxJFFkhbVSFr5Wjd/7XYlrWZi53XtLNDdmxM8L1P1fH8/NWoSZPMtzoB4cdispltk9cuPrNbRDd4Cr18dNq/5Nnn9fHEEfhjc3gazXxw6s+kWmf3yI7O3Nzy+OnRmr9vta/IW8vn7dOLfi2zi30v9gxo8yjGeenVIs0eG2SOj7JFA/2AnrXCVd5L0/Zw5gwvCl6XTQdna03UfveMawcHzBGeJqfzzs5rDVafxNc9u0RsQslT+cjrjaIfj0jJAo80DNDf9uJapECU7Q/cIn2AP8KmsQbLLiZ0yQOEeANQua5AeuncVoXIwt3Cyyn57YbQjOZEEC6KXGrSkSEczW0jbppJYnDrM2fx0vReHjgS+K0i8/IhELRK4hASWWwgSDxyKGeZpU1BU3uU/f58tQvqqVUToaOHIsnA5zruzkscGMqgVVr6YsPLlkqx8sVOs3Gri/+Wts+bWDcQ2U3YHzuzbSdnRLGVHs5QdzVJ22aLp5ZQdzVJ2NEvZ0SxlR7OUHV0lZUc/puxqdGDHU3b7lbHbOD63kHDYr5zd7iO05zm73QeorEH7lLFjh+2EyY5FuZAcwmFMMZEsnSRpMZtDgMwtybCN2RYSdgcOhCgBIW4JiJcfgagDgmwdiFeHDkS9adoMEM1iR5bFjiyLHVkWO2Z7KpVjR5LFjiSLHUkWO5IsdiSrxI5zPkI/lNhx4x8zbS12xB2n8J9Mv0oAW+RwLLBtYaG+QN1Zr6saWN7ul2ib8IrLA8e8FXF3C61gD9CaBJkzdI2VVI3uDXrhHqBXTeJUvYNdxasckfKDd/vWu4vU/LBzy9yerrRtG3f2DiNBtonEy0OX+wm36VZePh44t+W6ud0sguRZBMmzCJJnEWS2f3Y5gmRZBMmyCJJlESTLIki2SgTJPkaQNRmWHY0gJ3u27tfrx40DtPUocZ/wCfYAn0lcmGlQG89fO3a3IAr3AKLa4G9nEeqG4dBzp4OxV94rKLc00g2Wm20+Lk1DEmFS7JyIeZD2zrzeeTe8Qno5pwJk7lh7dLr0W9V5vYVPLwHc1Wo4S/FleIf4YpaOUdPl18eXyF2NL6MyX/Ku8ZYZQ4idcqZ+u6gVODNZ3ewr79J3g15FmxYtsrRgy9RgvqucX2kpuOlKS6Mqx/WWbIP0WNmibd0O5EY2SJ1uGc3vhn1dvIVUUBGD14sipny0/Ho7+07PxXor+0fRDlYpVWyDNFjMZkxmOXObYYdizhzb4Y60t7QJ55M3hY35Xldg/OWn+TiW9uX7qbovH2OMUIeCbXc44Va2XO8NNuYboX///X/Q/V9+QveGySP064/oCJEHNUFxuldjZgryBrjxXo3GMVpus751bdXIM9Fc32Z99etfssL6l6+9qKcQhjHiuT84S5A2ESM/SdR4emIKoc/QOIE/5uw/0xUyaz4OqSyRuYS/XI9/eHsJgzhxo0QbQL08ZtvuONJiwmLUIRKkW2YrjquFqbnNmW0TZoniprrNXZHw7rhohMh1+66pnLkDL875scpgTQTO6zcTYD5fgKe1n6Cp+EYriW9NXnfPxNfqEMoth3JMCZbg0shZ0rt4gHm9cOPXn5caYH4uawTvSCodxh3wsySjVDRXj/mjy89bGF1IurxuvUptei/YDQwvRYF4B+py6nvDftlbJBUx0DefhFcLVuZJJjVmcE4f3HAWZoZ/QNJVT0X9bs7NnUur3rmsXdIZoD/3+k+90Fi9jJ9DLxgkZym4K0JTXVYp4/CCWXSzodnqNLIcNDjdaVne1O+/CTR4bdC4s6FZ8HHcbGi2+nXYFBrJjd3Dc99DbRYZtwYZVkYGWBrEUIU2f+p84IUDrxu5X/w/UEsHCG5PkwOJEgAAv64AAFBLAQIUABQACAAIAHx0lEBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAfHSUQG5PkwOJEgAAv64AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAhEwAAAAA=" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "false" allowRescaling = "true" />
+==== Brytningsindex för några material ====
+{| border="1" style="border-collapse:collapse"
+|-----
+| &nbsp;Vakuum || &nbsp;1&nbsp;(exakt)&nbsp;
+|-----
+| &nbsp;Syrgas || &nbsp;1,00027
+|-----
+| &nbsp;Luft || &nbsp;1,00029
+|-----
+| &nbsp;Kvävgas || &nbsp;1,00030
+|-----
+| &nbsp;Vatten || &nbsp;1,33
+|-----
+| &nbsp;Etanol || &nbsp;1,36
+|-----
+| &nbsp;Bergkristall || &nbsp;1,46
+|-----
+| &nbsp;Terpentin || &nbsp;1,47
+|-----
+| &nbsp;Kronglas || &nbsp;1,51
+|-----
+| &nbsp;Flintglas || &nbsp;1,75
+|-----
+| &nbsp;Guanin || &nbsp;1,83
+|-----
+| &nbsp;Diamant || &nbsp;2,47
+|-----
+| &nbsp;Titandioxidkristall &nbsp; || &nbsp;3
+|}
+{{wp}}
 == Färger, s 204-207 ==
@@ Rad 150: / Rad 202: @@
 [[Fil:Light dispersion conceptual waves.gif|thumb|center]]
 [[File:RGB illumination.jpg|thumb|center|RGB illumination]]
+{{clear}}
+[[Bild:BYR color wheel.svg|thumb|Färghjul. En färgs komplementfärg återfinns på motsatt sida av cirkeln.]]
+Komplementfärg kan man säga är en färgs motsatsfärg. I vissa färgcirklar ligger dessa färger mitt emot varandra. När man blandar dessa två motsatsfärger uppstår en neutraliserad ton (grå).
+Ett objekt som diffusivt (spridande) reflekterar alla våglängder uppfattas som vit, medan ett objekt som absorberar alla våglängder uppfattas som svart.
+{{wp}
+Om föremålet absorberar en färg, exempelvis blå kommer det att uppfattas som att det har komplementfärgen, exempelvi orange.
 {{clear}}
 <youtube>7g0q1-Kkhvs</youtube>
 == Linser, s 208-211 ==
+=== Konvexa linser ===
 [[File:FocalLength.png|thumb|vv]]
+[[File:Convex lens diagram.svg|thumb|Convex lens diagram]]
+[[File:Lens (optics).png|thumb|Lens (optics)]]
+{{clear}}
+=== Konkava linser ===
+[[File:Concave lens.jpg|thumb|Concave lens]]
+{{clear}}
+=== [[Simulering av linser]] ===
+=== Länkar ===
 * [http://www.geogebrainstitut.se/resurser/ggb/raytracing.ggb Hur bilden skapas genom en lins]
 * [http://www.geogebratube.org/student/m4575 Concave convex lenses]
 <html><iframe src="http://phet.colorado.edu/sims/geometric-optics/geometric-optics_en.html" width="800" height="600"></iframe></html>
+{{clear}}
 == Linsens förstoring, s 212-215 ==
@@ Rad 175: / Rad 248: @@
 [[Image:Total internal reflection.PNG|total internal reflection]]
-== laboration ==
+== Laboration optik ==
+TEDT10 ni får göra laborationen på måndag morgon. Tyvärr har det dykt upp en konferens som jag måste närvara vid.
+Materialet finns i lådorna.
+Läs igenom hela instruktionen först.
+Dela in er i lagom stora grupper och labba.
+Var försiktiga, utrustningen är dyr.
+Jag finns i salen bredvid om ni har några viktiga frågor.
+== Synfel ==
+http://celebrate.ls.no/Norsk/Animasjoner/NMfag/linser_fokuseringsfeil.swf
 == repetition ==
+Titta på provet med lösningar nedan.
 == prov ==
+* [[Lösningar till optikprovet]]
+* [[Bedömningsmatris till optikprovet]]

Fysik A Optik: Skillnad mellan sidversioner

Nuvarande version från 15 juni 2012 kl. 22.09

Diverse

Kursnavet

GeoGebra-länkar

Hur gör man? - Wikimarkup

Vad är ljus?, s 189-197

Ljuskällor

ljusets hastighet

ljusstrålars utbredning

Kärnskugga och halvskugga

reflektion

Regelbunden reflektion

Diffus reflektion

Avbildning i plan spegel

Buktiga speglar

Konkava speglar

Länkar

Uppgift

Praktisk övning

Konvexa speglar

Förstoring

Ljusets brytning, s198-203

Ljusets brytning

Snells lag

Minnesregel

Snells lag

Läs mer

Totalreflektion

Brytningsindex

Reflektion, brytning och totalreflektion

Brytningsindex för några material

Färger, s 204-207

Linser, s 208-211

Konvexa linser

Konkava linser

Simulering av linser

Länkar

Linsens förstoring, s 212-215

Kameran och ögat, s 215-219

Optiska instrument, s 220-225

Optiska fibrer

Laboration optik

Synfel

repetition

prov

Navigeringsmeny

Sök