Övergripande kursplan för sannolikhetslära: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) (Ny sida: För godkänt ska du: • kunna ange sannolikheter för vanliga händelser i samband med spel Exempel Beräkna sannolikheten för att få en fyra om du kastar en tärning 30 gånger ...) |
Hakan (diskussion | bidrag) |
||
| (6 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
För godkänt ska du: | == För godkänt ska du: == | ||
• kunna ange sannolikheter för vanliga händelser i samband med spel | • kunna ange sannolikheter för vanliga händelser i samband med spel | ||
Exempel | Exempel | ||
Beräkna sannolikheten för att få en fyra om du kastar en tärning 30 gånger | Beräkna sannolikheten för att få en fyra om du kastar en tärning 30 gånger | ||
• kunna räkna ut sannolikheten för att vinna i ett lotteri | • kunna räkna ut sannolikheten för att vinna i ett lotteri | ||
Exempel | Exempel | ||
I ett lotteri med 4000 lotter finns det 200 vinster. Hur stor är sannolikheten att vinna? | |||
I ett lotteri med 4000 lotter finns det 200 vinster. Hur stor är sannolikheten att vinna? | |||
• kunna ange sannolikheten på tre sätt (bråk-, decimal- och procentform) | • kunna ange sannolikheten på tre sätt (bråk-, decimal- och procentform) | ||
Exempel | Exempel | ||
½ 0,5 50% | |||
½ 0,5 50% | |||
• förstå att sannolikheten P är ett tal mellan 0 och 1 | • förstå att sannolikheten P är ett tal mellan 0 och 1 | ||
Exempel | Exempel | ||
P=0 händelsen är omöjlig, den inträffar aldrig | |||
P=1 händelsen är säker, den inträffar varje gång | |||
För väl godkänt ska du: | == För väl godkänt ska du: == | ||
• kunna beräkna sannolikhet vid upprepade händelser | • kunna beräkna sannolikhet vid upprepade händelser | ||
Exempel | Exempel | ||
Hur stor är sannolikheten att få ”kung” två gånger i rad när du singlar slant? | |||
Hur stor är sannolikheten att få ”kung” två gånger i rad när du singlar slant? | |||
• kunna åskådliggöra sannolikheter vid upprepade händelser med hjälp av ett träddiagram | • kunna åskådliggöra sannolikheter vid upprepade händelser med hjälp av ett träddiagram | ||
Exempel | Exempel | ||
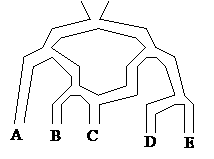
Du släpper ner 16 kulor i detta rörsystem. Hur kommer kulorna troligen att fördela sig i de fem burkarna? | Du släpper ner 16 kulor i detta rörsystem. Hur kommer kulorna troligen att fördela sig i de fem burkarna? | ||
[[Bild:Sannolkhetsexempel1.gif|rörsystem]] | |||
• känna till begreppet kombinatorik | • känna till begreppet kombinatorik | ||
Hur många olika tresiffriga tal kan du bilda av siffrorna 2, 5 och 8? Varje siffra får bara användas en gång i talen. | Hur många olika tresiffriga tal kan du bilda av siffrorna 2, 5 och 8? | ||
Varje siffra får bara användas en gång i talen. | |||
För mycket väl godkänt ska du kunna: | == För mycket väl godkänt ska du kunna: == | ||
Exempel | Exempel | ||
Olle tävlar i skytte. Varje skott ger mellan 0 och 10 poäng. I tävlingen sköt han 5 skott. Medelvärdet blev 8 och | Olle tävlar i skytte. Varje skott ger mellan 0 och 10 poäng. I tävlingen sköt han 5 skott. | ||
Medelvärdet blev 8 och medianvärdet 10. | |||
Diskutera hur Olle kan ha skjutit och redovisa alla möjlighterna. | |||
Exempel | Exempel | ||
Koden till ett kassaskåp består av fem tal mellan 0 och 9 i rätt ordning. Samma tal kan förekomma flera gånger. Hur många kombinationer måste den som har glömt sin kod i värsta fall pröva? | Koden till ett kassaskåp består av fem tal mellan 0 och 9 i rätt ordning. Samma tal kan förekomma flera gånger. | ||
Hur många kombinationer måste den som har glömt sin kod i värsta fall pröva? | |||
Nuvarande version från 19 januari 2009 kl. 22.00
För godkänt ska du:
• kunna ange sannolikheter för vanliga händelser i samband med spel
Exempel Beräkna sannolikheten för att få en fyra om du kastar en tärning 30 gånger
• kunna räkna ut sannolikheten för att vinna i ett lotteri
Exempel I ett lotteri med 4000 lotter finns det 200 vinster. Hur stor är sannolikheten att vinna?
• kunna ange sannolikheten på tre sätt (bråk-, decimal- och procentform)
Exempel ½ 0,5 50%
• förstå att sannolikheten P är ett tal mellan 0 och 1
Exempel P=0 händelsen är omöjlig, den inträffar aldrig P=1 händelsen är säker, den inträffar varje gång
För väl godkänt ska du:
• kunna beräkna sannolikhet vid upprepade händelser
Exempel Hur stor är sannolikheten att få ”kung” två gånger i rad när du singlar slant?
• kunna åskådliggöra sannolikheter vid upprepade händelser med hjälp av ett träddiagram
Exempel Du släpper ner 16 kulor i detta rörsystem. Hur kommer kulorna troligen att fördela sig i de fem burkarna?
• känna till begreppet kombinatorik
Hur många olika tresiffriga tal kan du bilda av siffrorna 2, 5 och 8? Varje siffra får bara användas en gång i talen.
För mycket väl godkänt ska du kunna:
Exempel Olle tävlar i skytte. Varje skott ger mellan 0 och 10 poäng. I tävlingen sköt han 5 skott. Medelvärdet blev 8 och medianvärdet 10. Diskutera hur Olle kan ha skjutit och redovisa alla möjlighterna.
Exempel Koden till ett kassaskåp består av fem tal mellan 0 och 9 i rätt ordning. Samma tal kan förekomma flera gånger. Hur många kombinationer måste den som har glömt sin kod i värsta fall pröva?