Lådan - en praktisk övning
Uppgift att tillverka en låda med störst volym
Tänk dig att du formar en låda genom att klippa bort lika stora kvadrater i hörnen av ett rektangulärt papper och därefter viker upp kanterna. Vad ska kvadraterna ha för sidlängd för att maximera lådans volym? Vi kan för klarhetens skull kalla papperssidorna a respektive b och kvadratens sida x.
Vi bekantar oss med problemet.
För att slippa detaljer och decimaler tänker vi oss ett papper som har sidorna 10 cm och 20 cm.
- Om vi klipper bort 1 cm i varje hörn blir botten på lådan [math]\displaystyle{ 8 * 18 cm^2 }[/math]. Volymen blir då [math]\displaystyle{ 8 * 18 * 1 cm^3 = 144 cm^3 }[/math].
- Om vi klipper bort 2 cm i varje hörn blir botten på lådan [math]\displaystyle{ 6 * 16 cm^2 }[/math]. Volymen blir då [math]\displaystyle{ 6 * 16 * 2 cm^3 = 96 * 2 = 192 cm^3 }[/math].
- Om vi klipper bort 3 cm i varje hörn blir botten på lådan [math]\displaystyle{ 4 * 14 cm^2 }[/math]. Volymen blir då [math]\displaystyle{ 4 * 14 * 3 cm^3 = 56 * 3 = 168 cm^3 }[/math].
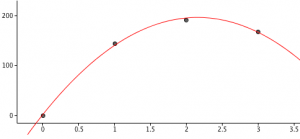
Nu ser vi att vi verkar ha en maxvolym om man klipper bort 2 cm. problemet är att vi inte vet om det är störst volym när man klipper bort exakt 2 cm. Det kan ju hända att lösningen är att klippa bort ett hörn med ett mått som anges i cm, mm och många decimaler därtill.
Vi kan nu ta våra värden på x och volym och rita en enkel graf.
Nu har vi begripit mer av hur problemet fungerar. Dags att vi ger oss in på det riktiga problemet.
Lösning
Papperets kanter har längderna a och b.
Lådans kanter har längderna a-2x och b-2x efter det att man har klippt bort hörnen. Hörnen har ju sidan x.
Man viker upp kanterna på lådan och kanterna är förstås x höga.
Lådans volym ges då av bottenarean multiplicerat med kantens höjd. Vi kan skriva ett uttryck för lådans volyn V(x).
- [math]\displaystyle{ V(x) = (a-2x)(b-2x) x }[/math]
För att få fram den maximala volyme ska vi derivera uttrycket för volymen och sätta derivatan lika med noll. Det kommer att ge oss en ekvation där lösningen är det x-värde som ger störstvolym.
Vi börjar med att förenkla uttrycket genom att multiplicera ihop parenteserna, mm.
- [math]\displaystyle{ V(x) = (a-2x)(b-2x) x = abx - 2 ax^2 - 2bx^2 + x^3 }[/math]
Om vi deriverar
- [math]\displaystyle{ V(x) = abx - 2 ax^2 - 2bx^2 + x^3 }[/math]
får vi
- [math]\displaystyle{ V'(x) = ab - 4 ax - 4bx + 3x^2 }[/math]
Då sätter vi derivatan lika med noll vilket betyder:
- [math]\displaystyle{ ab - 4 ax - 4bx + 3x^2 = 0 }[/math]
Det är en andragradsekvation som vi stuvar om så att den stämmer med pq-formeln:
- [math]\displaystyle{ x^2 - \frac {4}{3} (a - b) x + \frac {ab}{3} = 0 }[/math]
Lösningen är:
- [math]\displaystyle{ x = \frac {2}{3} (a - b) +- \sqrt{(\frac {2}{3} (a - b))^2 - \frac {ab}{3}} }[/math]
Den roten som ger vårt maximum är.
- [math]\displaystyle{ x = \frac {2}{3} (a - b) - \sqrt{(\frac {2}{3} (a - b))^2 - \frac {ab}{3}} }[/math]
Om man sätter a = 10 och b = 20 som i testet ovan får vi max vid [math]\displaystyle{ x = 5 - \frac {5}{\scrt{3}} \cong 2.11 }[/math]
Tips:
Wolfram Alpha ger en snygg lösning: med a = 20 och b = 10: http://www.wolframalpha.com/input/?i=maximum+%2820-2x%29%2810-2x%29x
Här är så en GGB som visar lösningen:
I denna GGB kan du se hur max inträffar där derivatan är lika med noll samt att tangenten i den punkten är helt horisontell.
Du kan även testa var max hamnar om du flyttar glidarna till andra mått på papperet (a och b kan variera från noll till A4-storlek).